引言 力扣提供海量题库,帮助你高效提升编程技能,轻松拿下世界 IT 名企 Dream Offer。本文作为博主的LeetCode刷题记录,包含基于C++的解题思路与完整代码以供参考学习。
来源:力扣(LeetCode)https://leetcode-cn.com
两数之和[1] 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素不能使用两遍。
你可以按任意顺序返回答案。
示例 1 输入:nums = [2,7,11,15], target = 9 输出:[0,1] 解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2 输入:nums = [3,2,4], target = 6 输出:[1,2]
示例 3 输入:nums = [3,3], target = 6 输出:[0,1]
提示 2 <= nums.length <= 103 $-10^9$ <= nums[i] <= $10^9$ $-10^9$ <= target <= $10^9$ 只会存在一个有效答案 默认模板 class Solution {public : vector<int > twoSum (vector<int >& nums, int target) { } };
题解 暴力枚举 这道题很像AOJ中的一道题,那时候我就用的这种二次循环的遍历方式枚举每一种情况。需要注意到每一个位于 x 之前的元素都已经和 x 匹配过,因此不需要再进行匹配。而每一个元素不能被使用两次,所以我们只需要在 x 后面的元素中寻找 target - x。
class Solution {public : vector<int > twoSum (vector<int >& nums, int target) { vector<int > v (2 ) ; for (int i = 0 ;i < nums.size ();i++){ for (int j = i + 1 ;j < nums.size ();j++){ if (nums[i] + nums[j] == target){ v[0 ] = i; v[1 ] = j; return v; } } } return v; } };
两数相加[2] 给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例1
输入:l1 = [2,4,3], l2 = [5,6,4] 输出:[7,0,8] 解释:342 + 465 = 807.
示例 2 输入:l1 = [0], l2 = [0] 输出:[0]
示例 3 输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9] 输出:[8,9,9,9,0,0,0,1]
提示 每个链表中的节点数在范围 [1, 100] 内 0 <= Node.val <= 9题目数据保证列表表示的数字不含前导零 模板 class Solution {public : ListNode* addTwoNumbers (ListNode* l1, ListNode* l2) { } };
题解 这道题涉及到了链表的知识。我一开始的想法是先把链表遍历导出到比较方便访问的数据结构比如vector然后再倒置最后相加,后面开始写伪代码的时候困难重重,比较难实现所以就放弃了这个思路。
之后参考了精选解题的思路,对于两个链表节点个数不同的情况我们可以选择将节点数较小的那个表补零,比如l1=[2,0,4,3]、l2=[5,6,8],此时l2少一个节点,那么我们就可以对l2补零为[5,6,8,0]使之节点数相同。
int len1 = 0 ,len2 = 0 ;ListNode* p = l1; ListNode* q = l2; while (p->next != NULL ){ len1++; p = p->next; } while (q->next != NULL ){ len2++; q = q->next; } ListNode* zero = len1 > len2 ? q : p; for (int i = 0 ;i < len1 - len2;i++){ zero->next = new ListNode (0 ); zero = zero->next; }
在l1与l2位数相同后该考虑的就是相加的问题,这个其实就简单很多了,设置一个用于进位的carry负责下一位的进制,而对于输出的链表l3而言sum%10就是它在该位置上的值。
class Solution {public : ListNode* addTwoNumbers (ListNode* l1, ListNode* l2) { int len1 = 0 ,len2 = 0 ; ListNode* p = l1; ListNode* q = l2; while (p->next != NULL ){ len1++; p = p->next; } while (q->next != NULL ){ len2++; q = q->next; } ListNode* zero = len1 > len2 ? q : p; for (int i = 0 ;i < len1 - len2;i++){ zero->next = new ListNode (0 ); zero = zero->next; } p = l1; q = l2; int carry = 0 ,sum = 0 ; ListNode* l3 = new ListNode (0 ); ListNode* r = l3; while (p != NULL && q != NULL ){ sum = carry + p->val + q->val; r->next = new ListNode (sum%10 ); carry = sum >= 10 ? 1 : 0 ; r = r->next; p = p->next; q = q->next; } return l3; } };
然而满怀欣喜的提交后倒在了1138 样例中,大家不妨先不往下翻,先带入该样例看看哪里出了问题。
输入: [2,4,9] [5,6,4,9] 输出: [7,0,4,1] 预期: [7,0,4,0,1]
一检查源码问题可太多了:
补零没有使用绝对值函数abs(),导致如果len1<len2不会补零而实际上我们需要补零 没有考虑最后一位的情况,如果还有进制会导致结果出错(少一个最高位位的1) 结果输出实际上是从l3->next开始的,最初始的节点并没有派上用场 /** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode() : val(0), next(nullptr) {} * ListNode(int x) : val(x), next(nullptr) {} * ListNode(int x, ListNode *next) : val(x), next(next) {} * }; */ class Solution { public: ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) { int len1 = 0,len2 = 0; ListNode* p = l1; ListNode* q = l2; while(p->next != NULL){ len1++; p = p->next; } while(q->next != NULL){ len2++; q = q->next; } ListNode* zero = len1 > len2 ? q : p; - for(int i = 0;i < len1 - len2;i++){ + for(int i = 0;i < abs(len1 - len2);i++){ zero->next = new ListNode(0); zero = zero->next; } p = l1; q = l2; int carry = 0,sum = 0; ListNode* l3 = new ListNode(0); ListNode* r = l3; while(p != NULL && q != NULL){ sum = carry + p->val + q->val; r->next = new ListNode(sum%10); carry = sum >= 10 ? 1 : 0; r = r->next; p = p->next; q = q->next; } + if(carry){ + r->next = new ListNode(1); + r = r->next; + } - return l3; + return l3->next; } };
无重复字符的最长子串[3] 给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1 输入: s = "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2 输入: s = "bbbbb" 输出: 1 解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3 输入: s = "pwwkew" 输出: 3 解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。 请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
示例 4 提示 0 <= s.length <= $5 * 10^4$ s 由英文字母、数字、符号和空格组成默认模板 class Solution {public : int lengthOfLongestSubstring (string s) } };
题解 本题属于典型的滑动窗口问题,这类问题的逻辑基本上是这样:
int left = 0 ,right = 0 ;while (right < s.size ()){ window.add (s[right]); right++; while (window needs shrink){ window.remove (s[left]); left++; } }
因为左右指针只遍历字符串一次,所以时间复杂度为$O(N)$,比字符串暴力算法要高效的多。对上面的逻辑再加以整理,labuladong总结出一套滑动算法的代码框架:
void slidingWindow (string s) unordered_map<char ,int > window; int left = 0 ,right = 0 ; while (right < s.size ()){ char c = s[right]; right++; ...... while (window needs shrink){ char d = s[left]; left++; ...... } } }
其中两处...表示更新窗口数据的地方,我们只需要在这里填入具体的窗口数据更新的逻辑即可,而且右移和左移的操作是完全对称的。
回到本题,很显然当window[c]的值大于1时窗口存在重复的字符,不满足题目要求,移动left缩小窗口。比较难理解的是res = max(res,right - left);,我们可以理解为一种另类的求最大值,虽然指针在不断滑动,但res与right-left求最大值保证了之前的最大值与现在可能超过的长度进行比较从而得出我们需要的最长子串。如果还有疑问或者不理解可以带入下面的求解过程体会:
(a)bcabcbb (ab)cabcbb (abc)abcbb abc(a)bcbb abc(ab)cbb abc(abc)bb abcabc(b)b abcabcb(b)
最后完整源码如下:
class Solution {public : int lengthOfLongestSubstring (string s) unordered_map<char ,int > window; int left = 0 ,right = 0 ; int res = 0 ; for (int i = 0 ;i < s.size ();i++){ char c = s[right++]; window[c]++; while (window[c] > 1 ){ char d = s[left++]; window[d]--; } res = max (res,right - left); } return res; } };
[未解决]寻找两个正序数组的中位数[4] 给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
示例 1 输入:nums1 = [1,3], nums2 = [2] 输出:2.00000 解释:合并数组 = [1,2,3] ,中位数 2
示例 2 输入:nums1 = [1,2], nums2 = [3,4] 输出:2.50000 解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
示例 3 输入:nums1 = [0,0], nums2 = [0,0] 输出:0.00000
示例 4 输入:nums1 = [], nums2 = [1] 输出:1.00000
示例 5 输入:nums1 = [2], nums2 = [] 输出:2.00000
提示 nums1.length == mnums2.length == n0 <= m <= 1000 0 <= n <= 1000 1 <= m + n <= 2000 $-10^6$ <= nums1[i], nums2[i] <= $10^6$ 进阶:你能设计一个时间复杂度为 O(log (m+n)) 的算法解决此问题吗?
默认模板 class Solution {public : double findMedianSortedArrays (vector<int >& nums1, vector<int >& nums2) } };
题解 最长回文子串[5] 给你一个字符串 s,找到 s 中最长的回文子串。
示例 1 输入:s = "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。
示例 2 示例 3 示例 4 提示 1 <= s.length <= 1000 s 仅由数字和英文字母(大写和/或小写)组成 默认模板 class Solution {public : string longestPalindrome (string s) { } };
题解 本题要求我们求出字符串中回文子串中长度最长的一个子串。
我们可以举两个回文串aa、babab来理解题目,首先回文串有a、b、aa、bab、aba、babab,可以观察到回文串有奇数和偶数两种情况,并且由于回文串对称的特性,我们应该不断判断字符串左右是否相同以保持这个对称的特性。
基于此我们可以先写出这个判断函数,内容就是以某个点为中心向左右两边发散,判断是否为回文串并返回最小的回文子串:
string traceMid2Side (string s,int left,int right) { while (left >= 0 && right <= s.length () - 1 && s[left] == s[right]){ left--; right++; } return s.substr (left + 1 ,right - left - 1 ); }
命令第一个元素为最后返回的结果res,如果没有第一个元素返回空字符串。之后遍历字符串,按刚才依次从中间向左右寻找是否有回文子串以临时变量tmp储存,并比较与res的长度。
两次调用traceMid2Side()是考虑到之前提到的奇偶问题,奇数情况左右都是i,偶数情况左边是i右边是i+1:
class Solution {public : string longestPalindrome (string s) { int len = s.length (); if (len == 0 ) return "" ; string res = s.substr (0 ,1 ); for (int i = 0 ;i <= len - 2 ;i++){ string tmp = traceMid2Side (s,i,i); if (tmp.length () > res.length ()) res = tmp; tmp = traceMid2Side (s,i,i + 1 ); if (tmp.length () > res.length ()) res = tmp; } return res; } string traceMid2Side (string s,int left,int right) { while (left >= 0 && right <= s.length () - 1 && s[left] == s[right]){ left--; right++; } return s.substr (left + 1 ,right - left - 1 ); } };
Z 字形变换[6] 将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 "PAYPALISHIRING" 行数为 3 时,排列如下:
P A H N A P L S I I G Y I R
之后,你的输出需要从左往右逐行读取,产生出一个新的字符串,比如:"PAHNAPLSIIGYIR"。
请你实现这个将字符串进行指定行数变换的函数:
string convert (string s, int numRows) ;
示例 1 输入:s = "PAYPALISHIRING", numRows = 3 输出:"PAHNAPLSIIGYIR"
示例 2 输入:s = "PAYPALISHIRING", numRows = 4 输出:"PINALSIGYAHRPI" 解释: P I N A L S I G Y A H R P I
示例 3 输入:s = "A", numRows = 1 输出:"A"
提示 1 <= s.length <= 100 s 由英文字母(小写和大写)、',' 和 '.' 组成1 <= numRows <= 1000 默认模板 class Solution {public : string convert (string s, int numRows) { } };
题解 本题是一个找规律的题,首先我们先观察给出样例的Z形排列中下标的变化,可以发现行数的变化是周期性的:0-1-2-1-0-……:
PAYPALISHIRING 0: P(0) A(4) H(8) N(12) 1: A(1) P(3) L(5) S(7) I(9) I(11) G(13) 2: Y(2) I(6) R(10) PAHKAPLSIIGYIR
所以我们就以行数的周期反复为突破点,用字符串数组分别存储每行的字符串。在遍历字符串s时根据行数由0到numRows再到0,最后以+合并进res字符串即可:
class Solution {public : string convert (string s, int numRows) { int i = 0 ; string res,z[numRows]; while (i < s.length ()){ for (int j = 0 ; j < numRows && i < s.length (); ++j) { z[j] += s[i++]; } for (int k = numRows - 2 ; k > 0 && i < s.length (); --k) { z[k] += s[i++]; } } for (int j = 0 ; j < numRows; ++j) { res += z[j]; } return res; } };
整数反转[7] 给你一个 32 位的有符号整数 x ,返回 x 中每位上的数字反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 $[−2^{31}, 2^{31} − 1]$ ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
示例 1 示例 2 示例 3 示例 4 提示 $-2^{31}$ <= x <= $2^{31} - 1$ 默认模板 class Solution {public : int reverse (int x) } };
题解 本题考查的是C++字符串转换,主要使用了两个库函数:
reverse reverse()函数功能是逆序(或反转),多用于字符串、数组、容器,头文件是#include <algorithm>。reverse()函数用于反转在[first,last)范围内的顺序(包括first指向的元素,不包括last指向的元素),reverse()函数无返回值。
举个例子来体会一下这个函数的用法:
string str="hello world , hi" ; reverse (str.begin (),str.end ());vector<int > v = {5 ,4 ,3 ,2 ,1 }; reverse (v.begin (),v.end ());
stoll stoll()函数功能是将字符串转换为long long,也就是解析str将其内容解释为指定基数的整数,并将其作为long long类型的值返回。如果idx不是空指针,则该函数还将idx的值设置为数字后str中第一个字符的位置。
long long stoll (const string& str, size_t * idx = 0 , int base = 10 ) long long stoll (const wstring& str, size_t * idx = 0 , int base = 10 )
完整源码如下:
class Solution {public : int reverse (int x) string s = to_string (x); if (s[0 ] == '-' ){ std::reverse (s.begin () + 1 ,s.end ()); } else { std::reverse (s.begin (),s.end ()); } long long int tmp = stoll (s); if (tmp > pow (2 ,31 ) - 1 || tmp < -pow (2 ,31 )) return 0 ; return tmp; } };
[未解决]字符串转换整数 (atoi)[8] 请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C++ 中的 atoi 函数)。
函数 myAtoi(string s) 的算法如下:
读入字符串并丢弃无用的前导空格 检查下一个字符(假设还未到字符末尾)为正还是负号,读取该字符(如果有)。 确定最终结果是负数还是正数。 如果两者都不存在,则假定结果为正。 读入下一个字符,直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。 将前面步骤读入的这些数字转换为整数(即,”123” -> 123, “0032” -> 32)。如果没有读入数字,则整数为 0 。必要时更改符号(从步骤 2 开始)。 如果整数数超过 32 位有符号整数范围 [−231, 231 − 1] ,需要截断这个整数,使其保持在这个范围内。具体来说,小于 −231 的整数应该被固定为 −231 ,大于 231 − 1 的整数应该被固定为 231 − 1 。 返回整数作为最终结果。 注意:
本题中的空白字符只包括空格字符 ' ' 。 除前导空格或数字后的其余字符串外,请勿忽略 任何其他字符。 示例 1 输入:s = "42" 输出:42 解释:加粗的字符串为已经读入的字符,插入符号是当前读取的字符。 第 1 步:"42"(当前没有读入字符,因为没有前导空格) ^ 第 2 步:"42"(当前没有读入字符,因为这里不存在 '-' 或者 '+') ^ 第 3 步:"42"(读入 "42") ^ 解析得到整数 42 。 由于 "42" 在范围 [-231, 231 - 1] 内,最终结果为 42 。
示例 2 输入:s = " -42" 输出:-42 解释: 第 1 步:" -42"(读入前导空格,但忽视掉) ^ 第 2 步:" -42"(读入 '-' 字符,所以结果应该是负数) ^ 第 3 步:" -42"(读入 "42") ^ 解析得到整数 -42 。 由于 "-42" 在范围 [-231, 231 - 1] 内,最终结果为 -42 。
示例 3 输入:s = "4193 with words" 输出:4193 解释: 第 1 步:"4193 with words"(当前没有读入字符,因为没有前导空格) ^ 第 2 步:"4193 with words"(当前没有读入字符,因为这里不存在 '-' 或者 '+') ^ 第 3 步:"4193 with words"(读入 "4193";由于下一个字符不是一个数字,所以读入停止) ^ 解析得到整数 4193 。 由于 "4193" 在范围 [-231, 231 - 1] 内,最终结果为 4193 。
示例 4 输入:s = "words and 987" 输出:0 解释: 第 1 步:"words and 987"(当前没有读入字符,因为没有前导空格) ^ 第 2 步:"words and 987"(当前没有读入字符,因为这里不存在 '-' 或者 '+') ^ 第 3 步:"words and 987"(由于当前字符 'w' 不是一个数字,所以读入停止) ^ 解析得到整数 0 ,因为没有读入任何数字。 由于 0 在范围 [-231, 231 - 1] 内,最终结果为 0 。
示例 5 输入:s = "-91283472332" 输出:-2147483648 解释: 第 1 步:"-91283472332"(当前没有读入字符,因为没有前导空格) ^ 第 2 步:"-91283472332"(读入 '-' 字符,所以结果应该是负数) ^ 第 3 步:"-91283472332"(读入 "91283472332") ^ 解析得到整数 -91283472332 。 由于 -91283472332 小于范围 [-231, 231 - 1] 的下界,最终结果被截断为 -231 = -2147483648 。
提示 0 <= s.length <= 200s 由英文字母(大写和小写)、数字(0-9)、' '、'+'、'-' 和 '.' 组成默认模板 class Solution {public : int myAtoi (string s) } };
题解 盛最多水的容器[11] 给你 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明: 你不能倾斜容器。
示例1
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例2 示例3 输入:height = [4,3,2,1,4] 输出:16
示例4 提示 n = height.length2 <= n <= 3 * $10^4$ 0 <= height[i] <= 3 * $10^4$ 模板 class Solution {public : int maxArea (vector<int >& height) };
题解 指针代表的是 可以作为容器边界的所有位置的范围。在一开始,双指针指向数组的左右边界,表示 数组中所有的位置都可以作为容器的边界,因为我们还没有进行过任何尝试。在这之后,我们每次将 对应的数字较小的那个指针 往 另一个指针 的方向移动一个位置,就表示我们认为 这个指针不可能再作为容器的边界了。
class Solution {public : int maxArea (vector<int >& height) int i = 0 , j = height.size () - 1 ; while (i < j) { if (height[i + 1 ] > height[i]) i++; if (height[j - 1 ] > height[j]) j--; } return (j - i) * min (height[i], height[j]); } };
三数之和[15] 给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意 :答案中不可以包含重复的三元组。
示例 1 输入:nums = [-1,0,1,2,-1,-4] 输出:[[-1,-1,2],[-1,0,1]]
示例 2 示例 3 提示 0 <= nums.length <= 3000 $-10^5$ <= nums[i] <= $10^5$ 模板 class Solution {public : vector<vector<int >> threeSum (vector<int >& nums) { };
题解 枚举第一个数,然后用双指针确定另外两个数。注意去重:
class Solution {public : vector<vector<int >> threeSum (vector<int >& nums) { vector<vector<int >> res; sort (nums.begin (), nums.end ()); for (int k = 0 ; k < nums.size (); k++) { int i = k + 1 ; int j = nums.size () - 1 ; if (k > 0 && nums[k] == nums[k - 1 ]) continue ; while (i < j) { if (nums[i] + nums[j] + nums[k] == 0 ) { res.push_back (vector<int >{nums[k], nums[i], nums[j]}); i++; j--; while (i < j && nums[i] == nums[i - 1 ]) i++; while (i < j && nums[j] == nums[j + 1 ]) j--; } else if (nums[i] + nums[j] + nums[k] < 0 ) { i++; } else { j--; } } } return res; } };
删除链表的倒数第 N 个结点[19] 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
进阶: 你能尝试使用一趟扫描实现吗?
示例1
输入:head = [1,2,3,4,5], n = 2 输出:[1,2,3,5]
示例 2 输入:head = [1], n = 1 输出:[]
示例3 输入:head = [1,2], n = 1 输出:[1]
提示 链表中结点的数目为 sz 1 <= sz <= 30 0 <= Node.val <= 100 1 <= n <= sz 模板 class Solution {public : ListNode* removeNthFromEnd (ListNode* head, int n) { } };
题解 正数第n到末尾的距离和倒数第n到开始的距离相同
class Solution {public : ListNode* removeNthFromEnd (ListNode* head, int n) { ListNode* dummy = new ListNode (0 , head); ListNode* fast = head; ListNode* slow = dummy; for (int i = 0 ; i < n; i++) fast = fast->next; while (fast) { fast = fast->next; slow = slow->next; } slow->next = slow->next->next; ListNode* ans = dummy->next; delete dummy; return ans; } };
有效的括号[20] 给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合 左括号必须以正确的顺序闭合 示例 1 示例 2 示例 3 示例 4 示例 5 提示 1 <= s.length <= 10^4s 仅由括号 '()[]{}' 组成模板 class Solution {public : bool isValid (string s) } };
题解 不能忘了扫描过的左括号,它们等着被匹配,用一个容器暂存——为什么是栈?
当遇到右括号时,我们期待它匹配「最近出现 的左括号」,于是容器中的「最近出现的左括号」不用等待匹配了,可以离开容器。它是「后进」的,现在「先出」,所以是栈。 像“对对碰”,匹配了就拿掉,如果最后清空了栈,则有效。如果栈中还剩左括号未匹配,则无效。
class Solution {public : bool isValid (string s) stack<char > st; for (char ch: s) { if (st.empty ()) st.push (ch); else if (ch == '(' || ch == '{' || ch == '[' ) st.push (ch); else { char top = st.top (); if ((top == '(' && ch == ')' ) || (top == '[' && ch == ']' ) || (top == '{' && ch == '}' )) st.pop (); else return false ; } } if (!st.empty ()) return false ; return true ; } };
删除有序数组中的重复项[26] 给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
说明 为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
int len = removeDuplicates (nums);for (int i = 0 ; i < len; i++) { print (nums[i]); }
示例1 输入:nums = [1,1,2] 输出:2, nums = [1,2] 解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例2 输入:nums = [0,0,1,1,1,2,2,3,3,4] 输出:5, nums = [0,1,2,3,4] 解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
提示 0 <= nums.length <= 3 * $10^4$ $-10^4$ <= nums[i] <= $10^4$ nums 已按升序排列模板 class Solution {public : int removeDuplicates (vector<int >& nums) } };
题解 此题要求我们删除重复字符,要注意的是去重之后元素的相对位置不能改变,比如 [1, 2, 2, 3] 去重后是 [1, 2, 3],而不能是 [1, 3, 2]。既然输入数组是排好序的,那么对于每段重复元素,他们必定是相连的,我们只需要记录头元素即可,然后依次记录下那些互不重合的元素,就能解决此题了。这种需要依次记录下所需要元素的问题,就能完全使用同向指针的套路来解决,以下是解题步骤和代码:
class Solution {public : int removeDuplicates (vector<int >& nums) int i = 0 , j = 0 ; while (j < nums.size ()) { if (i == 0 || nums[j] != nums[i - 1 ]) nums[i++] = nums[j++]; else j++; } return i; } };
简单来说,[0 ~ i) 区间的元素是我们决定留下来的元素,i 指向的位置需要放入的是下一个不重复元素,j 指针是用来遍历整个数组的。在遍历过程中,如果 array[j] 和 array[i – 1] 不同,代表出现了一个新的不重复元素,那么就将新元素赋给 array[i],否则向右移动 j 指针,直到 j 指针遍历完整个数组为止。
接雨水[42] 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例1
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例2 输入:height = [4,2,0,3,2,5] 输出:9
提示 n == height.length0 <= n <= 3 * $10^4$ 0 <= height[i] <= $10^5$ 模板 class Solution {public : int trap (vector<int >& height) } };
题解 这道题真正难点在于: 在一个位置能容下的雨水量等于它左右两边柱子最大高度的最小值减去它的高度.比如下图所示,
位置 i 能容下雨水量:min(3,1) - 0 = 1
所以,问题就变成了:如何找所有位置的左右两边的柱子的最大值?
这里我们沿用11题盛最多水容器的思路,用双指针遍历数组一次即可:
class Solution {public : int trap (vector<int >& height) int i = 0 , j = height.size () - 1 ; int area = 0 , left = 0 , right = 0 ; while (i < j) { left = max (left, height[i]); right = max (right, height[j]); if (height[i] < height[j]) { area += left - height[i]; i++; } else { area += right - height[j]; j--; } } return area; } };
字母异位词分组[49] 给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的字母得到的一个新单词,所有源单词中的字母通常恰好只用一次。
示例 1 输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"] 输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
示例 2 输入: strs = [""] 输出: [[""]]
示例 3 输入: strs = ["a"] 输出: [["a"]]
提示 1 <= strs.length <= 10^40 <= strs[i].length <= 100strs[i] 仅包含小写字母模板 class Solution {public : vector<vector<string>> groupAnagrams (vector<string>& strs) { } };
题解 遍历字符串,将每个字符串按照字符字典序排序后得到一个新的字符串,将相同的新字符串放在哈希表的同一个 key 对应 value 列表中。
key value "aet"["eat", "tea", "ate"]"ant"["tan", "nat"]"abt"["bat"]
最后返回哈希表的 value 列表即可。
class Solution {public : vector<vector<string>> groupAnagrams (vector<string>& strs) { vector<vector<string>> res; unordered_map<string, vector<string>> hash (strs.size ()); for (auto str: strs) { string key = str; sort (key.begin (), key.end ()); hash[key].emplace_back (str); } for (auto it = hash.begin (); it != hash.end (); it++) { res.emplace_back (it->second); } return res; } };
二进制求和[67] 给你两个二进制字符串,返回它们的和(用二进制表示)。
输入为 非空 字符串且只包含数字 1 和 0。
示例 1 输入: a = "11", b = "1" 输出: "100"
示例 2 输入: a = "1010", b = "1011" 输出: "10101"
提示 每个字符串仅由字符 ‘0’ 或 ‘1’ 组成 1 <= a.length, b.length <= 10^4 字符串如果不是 “0” ,就都不含前导零 模板 class Solution {public : string addBinary (string a, string b) { } };
题解 模拟笔算加法的过程,注意进位:
class Solution {public : string addBinary (string a, string b) { string res; int carry = 0 ; int i = a.size () - 1 ; int j = b.size () - 1 ; while (i >= 0 || j >= 0 ) { int digitA = i >= 0 ? a.at (i--) - '0' : 0 ; int digitB = j >= 0 ? b.at (j--) - '0' : 0 ; int sum = digitA + digitB + carry; carry = sum >= 2 ? 1 : 0 ; sum = sum >= 2 ? sum - 2 : sum; res += to_string (sum); } if (carry == 1 ) res.push_back ('1' ); reverse (res.begin (), res.end ()); return res; } };
删除有序数组中的重复项 II[80] 给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使每个元素 最多出现两次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
说明 为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
int len = removeDuplicates (nums);for (int i = 0 ; i < len; i++) { print (nums[i]); }
示例 1 输入:nums = [1,1,1,2,2,3] 输出:5, nums = [1,1,2,2,3] 解释:函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3 。 不需要考虑数组中超出新长度后面的元素。
示例 2 输入:nums = [0,0,1,1,1,1,2,3,3] 输出:7, nums = [0,0,1,1,2,3,3] 解释:函数应返回新长度 length = 7, 并且原数组的前五个元素被修改为 0, 0, 1, 1, 2, 3, 3 。 不需要考虑数组中超出新长度后面的元素。
提示 1 <= nums.length <= 3 * $10^4$ $-10^4$ <= nums[i] <= $10^4$ nums 已按升序排列模板 class Solution {public : int removeDuplicates (vector<int >& nums) } };
题解 题目大意:一个有序数组中,让每个数字最多出现两次,返回一个 n ,使得数组的前 n 个元素就是结果。需要在输入数组上原地修改。
今天这个题目是 26. 删除有序数组中的重复项 的进阶,可以先做一下 26 题。
注意是原地修改,那么肯定就需要一个指针指向当前即将放置元素的位置,需要另外一个指针向后遍历所有元素,所以「双指针」解法就呼之欲出了。如果能想到双指针解法,后面的分析也就顺理成章。
慢指针 slow : 指向当前即将放置元素的位置;则 slow - 1 是刚才已经放置了元素的位置。快指针 fast : 向后遍历所有元素;因为最多允许两个重复元素,并且 slow - 2 位置是上上次放置了元素的位置,所以让 nums[fast] 跟 nums[slow - 2] 进行比较。每次都是只允许最多两个元素出现重复,这两个元素的位置在 slow - 1 和 slow - 2.
请看下面的动图展示,一图胜千言。图中红色表示已经放置了正确元素的位置,绿色表示当前元素被修改了。
class Solution {public : int removeDuplicates (vector<int >& nums) if (nums.size () <= 2 ) return nums.size (); int i = 2 , j = 2 ; while (j < nums.size ()) { if (nums[j] != nums[i - 2 ]) { nums[i] = nums[j]; i++; } j++; } return i; } };
柱状图中最大的矩形[84] 给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1
输入:heights = [2,1,5,6,2,3] 输出:10 解释:最大的矩形为图中红色区域,面积为 10
示例 2
提示 1 <= heights.length <=10^50 <= heights[i] <= 10^4模板 class Solution {public : int largestRectangleArea (vector<int >& heights) } };
题解 我们可以遍历每根柱子,以当前柱子 i 的高度作为矩形的高,那么矩形的宽度边界即为向左找到第一个高度小于当前柱体 i 的柱体,向右找到第一个高度小于当前柱体 i 的柱体。
对于每个柱子我们都如上计算一遍以当前柱子作为高的矩形面积,最终比较出最大的矩形面积即可。
我们遍历每个柱体,若当前的柱体高度大于等于栈顶柱体的高度,就直接将当前柱体入栈,否则若当前的柱体高度小于栈顶柱体的高度,说明当前栈顶柱体找到了右边的第一个小于自身的柱体,那么就可以将栈顶柱体出栈来计算以其为高的矩形的面积了。
class Solution {public : int largestRectangleArea (vector<int >& heights) int maxarea = 0 ; stack<int > s; heights.insert (heights.begin (), 0 ); heights.push_back (0 ); for (int i = 0 ; i < heights.size (); i++) { while (!s.empty () && heights[i] < heights[s.top ()]) { int h = heights[s.top ()]; s.pop (); maxarea = max (maxarea, h * (i - s.top () - 1 )); } s.push (i); } return maxarea; } };
反转链表 II[92] 给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
进阶: 你可以使用一趟扫描完成反转吗?
示例1
输入:head = [1,2,3,4,5], left = 2, right = 4 输出:[1,4,3,2,5]
示例2 输入:head = [5], left = 1, right = 1 输出:[5]
提示 链表中节点数目为 n 1 <= n <= 500 -500 <= Node.val <= 500 1 <= left <= right <= n 模板 class Solution {public : ListNode* reverseBetween (ListNode* head, int left, int right) { } };
题解 class Solution { int pos = 0 ; public : ListNode* reverseBetween (ListNode* head, int left, int right) { pos++; if (pos == right || head->next == nullptr ) return head; else if (pos < left) { head->next = reverseBetween (head->next, left, right); return head; } else { ListNode* res = reverseBetween (head->next, left, right); ListNode* tmp = head->next->next; head->next->next = head; head->next = tmp; return res; } } };
只出现一次的数字 II[137] 给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。
示例 1 示例 2 输入:nums = [0,1,0,1,0,1,99] 输出:99
提示 1 <= nums.length <= 3 * $10^4$ $-2^{31}$ <= nums[i] <= $2^{31}$ - 1 nums 中,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 进阶 :你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
模板 class Solution {public : int singleNumber (vector<int >& nums) } };
题解 统计所有数字每个位中 1 出现的次数,对于某个位,1 出现的次数一定是 3 的倍数 +1 或 0。对这个数 %3 得到的结果就是那个出现一次的数字在该位上的值:
class Solution {public : int singleNumber (vector<int >& nums) vector<int > bit (32 ) ; for (int num : nums) for (int i = 0 ; i < 32 ; i++) bit[i] += (num >> (31 - i)) & 1 ; int res = 0 ; for (int i = 0 ; i < 32 ; i++) res = (res << 1 ) + bit[i] % 3 ; return res; } };
环形链表[141] 给定一个链表,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
如果链表中存在环,则返回 true 。 否则,返回 false 。
进阶:
你能用 *O(1)*(即,常量)内存解决此问题吗?
示例1
输入:head = [3,2,0,-4], pos = 1 输出:true 解释:链表中有一个环,其尾部连接到第二个节点。
示例2
输入:head = [1,2], pos = 0 输出:true 解释:链表中有一个环,其尾部连接到第一个节点。
示例3
输入:head = [1], pos = -1 输出:false 解释:链表中没有环。
提示 链表中节点的数目范围是 [0, 104] $-10^5$ <= Node.val <= $10^5$ pos 为 -1 或者链表中的一个 有效索引 模板 class Solution {public : bool hasCycle (ListNode *head) } };
题解 本方法需要读者对「Floyd 判圈算法」(又称龟兔赛跑算法)有所了解。
假想「乌龟」和「兔子」在链表上移动,「兔子」跑得快,「乌龟」跑得慢。当「乌龟」和「兔子」从链表上的同一个节点开始移动时,如果该链表中没有环,那么「兔子」将一直处于「乌龟」的前方;如果该链表中有环,那么「兔子」会先于「乌龟」进入环,并且一直在环内移动。等到「乌龟」进入环时,由于「兔子」的速度快,它一定会在某个时刻与乌龟相遇,即套了「乌龟」若干圈。
我们可以根据上述思路来解决本题。具体地,我们定义两个指针,一快一满。慢指针每次只移动一步,而快指针每次移动两步。初始时,慢指针在位置 head,而快指针在位置 head.next。这样一来,如果在移动的过程中,快指针反过来追上慢指针,就说明该链表为环形链表。否则快指针将到达链表尾部,该链表不为环形链表。
class Solution {public : bool hasCycle (ListNode *head) ListNode* i = head, *j = head; while (j != nullptr && j->next != nullptr ) { i = i->next; j = j->next->next; if (i == j) return true ; } return false ; } };
环形链表 II[142] 给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递 ,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1
输入:head = [3,2,0,-4], pos = 1 输出:返回索引为 1 的链表节点 解释:链表中有一个环,其尾部连接到第二个节点。
示例 2
输入:head = [1,2], pos = 0 输出:返回索引为 0 的链表节点 解释:链表中有一个环,其尾部连接到第一个节点。
示例 3
输入:head = [1], pos = -1 输出:返回 null 解释:链表中没有环。
提示 链表中节点的数目范围在范围 [0, 10^4] 内 -10^5 <= Node.val <= 10^5pos 的值为 -1 或者链表中的一个有效索引进阶: 你是否可以使用 O(1) 空间解决此题?
模板 class Solution {public : ListNode *detectCycle (ListNode *head) { } };
题解 先利用快慢指针判断链表是否有环,没有环则直接返回 null。
若链表有环,我们分析快慢相遇时走过的距离:
我们会发现:从相遇点到入环点的距离加上 $n-1$ 圈的环长,恰好等于从链表头部到入环点的距离。
class Solution {public : ListNode *detectCycle (ListNode *head) { ListNode* slow = head; ListNode* fast = head; while (true ) { if (fast == nullptr || fast->next == nullptr ) return nullptr ; slow = slow->next; fast = fast->next->next; if (fast == slow) break ; } fast = head; while (slow != fast) { slow = slow->next; fast = fast->next; } return fast; } };
重排链表[143] 给定一个单链表 L 的头节点 head,单链表 L 表示为:
L0 → L1 → … → Ln - 1 → Ln
请将其重新排列后变为:
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例 1
输入:head = [1,2,3,4] 输出:[1,4,2,3]
示例 2
输入:head = [1,2,3,4,5] 输出:[1,5,2,4,3]
提示 链表的长度范围为 [1, 5 * 104] 1 <= node.val <= 1000模板 class Solution {public : void reorderList (ListNode* head) } };
题解 相当于这 3 道问题,只需要 5 行代码将它们组合:
class Solution {public : void reorderList (ListNode* head) ListNode* dummy = new ListNode (); dummy->next = head; ListNode* slow = dummy; ListNode* fast = dummy; while (fast && fast->next) { slow = slow->next; fast = fast->next->next; } ListNode* cur = dummy->next; ListNode* mid = slow->next; slow->next = nullptr ; mid = reverseList (mid); while (mid) { ListNode* tmp = cur->next; cur->next = mid; cur = cur->next; mid = mid->next; cur->next = tmp; cur = cur->next; } } ListNode* reverseList (ListNode* head) { ListNode* cur = head; ListNode* pre = nullptr ; ListNode* succ = nullptr ; while (cur) { succ = cur->next; cur->next = pre; pre = cur; cur = succ; } return pre; } };
逆波兰表达式求值[150] 根据 逆波兰表示法 ,求表达式的值。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
整数除法只保留整数部分。 给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。 示例 1 输入:tokens = ["2","1","+","3","*"] 输出:9 解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2 输入:tokens = ["4","13","5","/","+"] 输出:6 解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3 输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"] 输出:22 解释: 该算式转化为常见的中缀算术表达式为: ((10 * (6 / ((9 + 3) * -11))) + 17) + 5 = ((10 * (6 / (12 * -11))) + 17) + 5 = ((10 * (6 / -132)) + 17) + 5 = ((10 * 0) + 17) + 5 = (0 + 17) + 5 = 17 + 5 = 22
提示 1 <= tokens.length <= 10^4tokens[i] 要么是一个算符("+"、"-"、"*" 或 "/"),要么是一个在范围 [-200, 200] 内的整数逆波兰表达式 :
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
平常使用的算式则是一种中缀表达式,如 ( 1 + 2 ) * ( 3 + 4 ) 该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 逆波兰表达式主要有以下两个优点:
去掉括号后表达式无歧义,上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果 适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中 模板 class Solution {public : int evalRPN (vector<string>& tokens) } };
题解 利用栈存储运算数,每次遇到符号,对栈顶两个元素进行运算。
class Solution {public : int evalRPN (vector<string>& tokens) stack<int > s; for (string& t: tokens) { if (isNumber (t)) { s.push (stoi (t)); } else { int a = s.top (); s.pop (); int b = s.top (); s.pop (); if (t[0 ] == '+' ) s.push (a + b); else if (t[0 ] == '-' ) s.push (b - a); else if (t[0 ] == '*' ) s.push (a * b); else s.push (b / a); } } return s.top (); } bool isNumber (string s) if (s.size () > 1 || (s[0 ] >= '0' && s[0 ] <='9' )) return true ; return false ; } };
最小栈[155] 设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
push(x) —— 将元素 x 推入栈中pop() —— 删除栈顶的元素top() —— 获取栈顶元素getMin() —— 检索栈中的最小元素示例 输入: ["MinStack","push","push","push","getMin","pop","top","getMin"] [[],[-2],[0],[-3],[],[],[],[]] 输出: [null,null,null,null,-3,null,0,-2] 解释: MinStack minStack = new MinStack(); minStack.push(-2); minStack.push(0); minStack.push(-3); minStack.getMin(); --> 返回 -3. minStack.pop(); minStack.top(); --> 返回 0. minStack.getMin(); --> 返回 -2.
提示 pop、top 和 getMin 操作总是在 非空栈 上调用。模板 class MinStack {public : MinStack () { } void push (int val) } void pop () } int top () } int getMin () } };
题解 此题要求写一个栈,与普通栈不同的是多出了一个获取最小值的方法。由于栈比较简单,这里就不多说了,主要还是说说怎么以 O(1) 的时间复杂度查找栈中的最小值。
使用一个变量 min 记录每次栈中的最小值,每次有元素进栈都对 min 进行更新。 为了解决出栈对最小值的更新,可以设定一个辅助栈,栈顶表示当前数据栈中的最小值,每次有元素入栈,就将当前最小值入辅助栈。出栈时,辅助栈也要将栈顶元素出栈,这就解决了出栈时的最小值更新问题。 push :将数据入栈的同时,更新最小值。如果入栈元素大于辅助栈顶元素(也就是元素入栈前,数据栈中的最小值),则最小值依旧是数据栈原来的最小值,否则将元素入辅助栈。
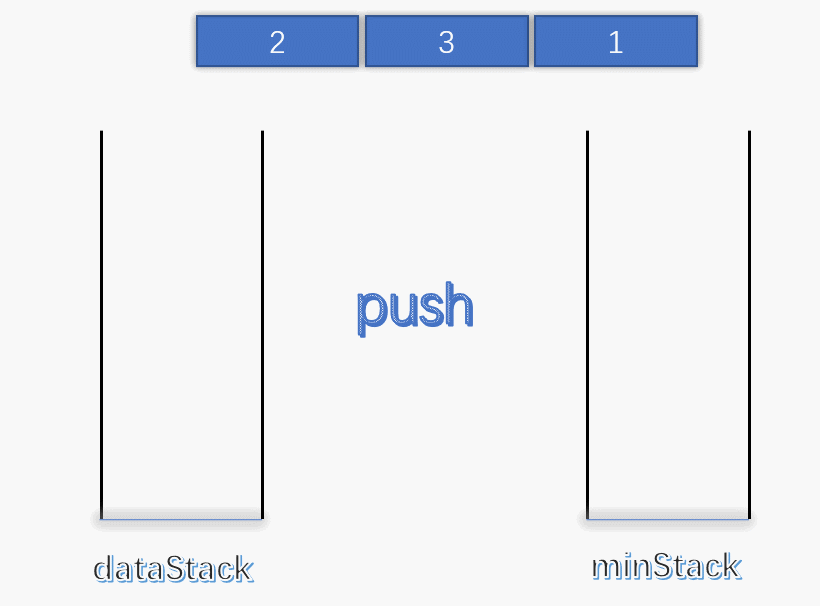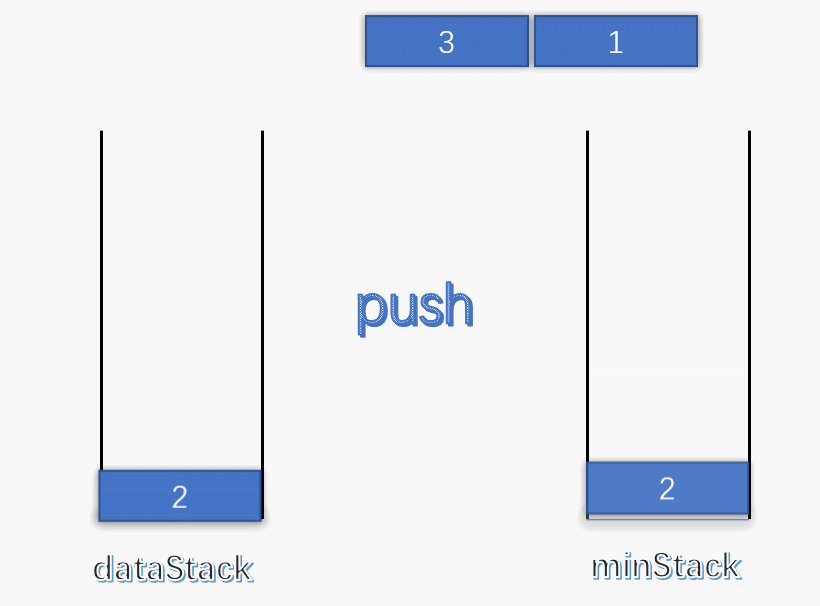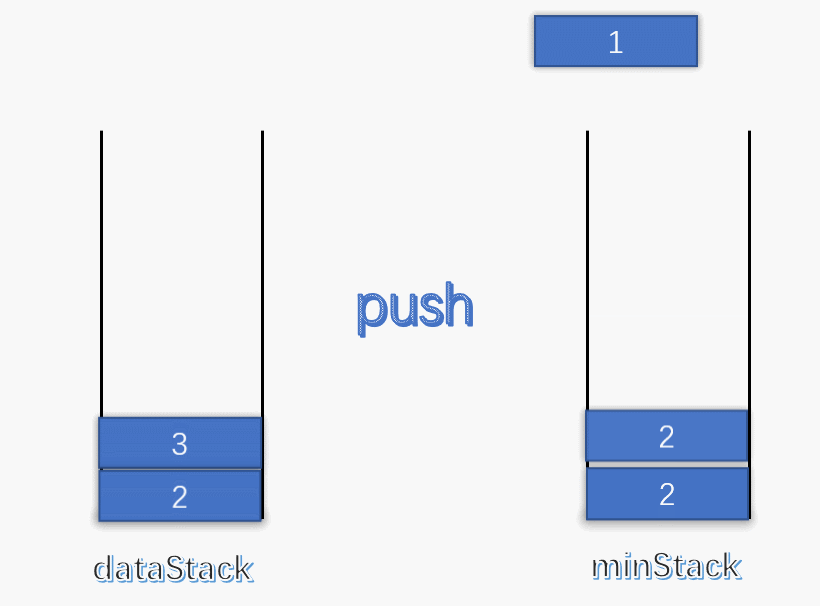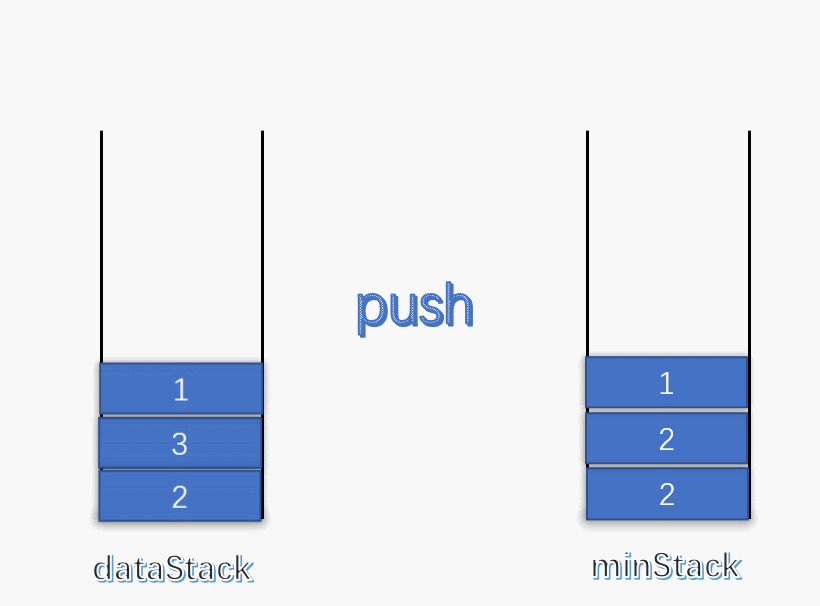
pop :将数据栈和辅助栈的栈顶元素同时出栈,保持辅助栈的栈顶元素是数据栈中的最小值。
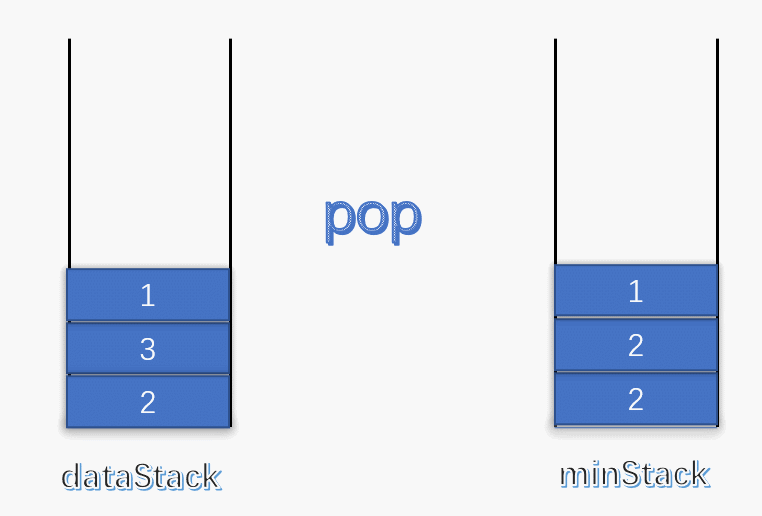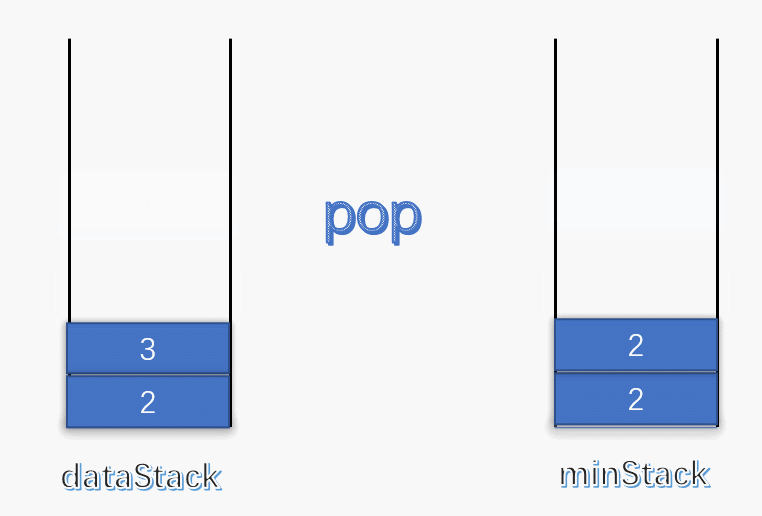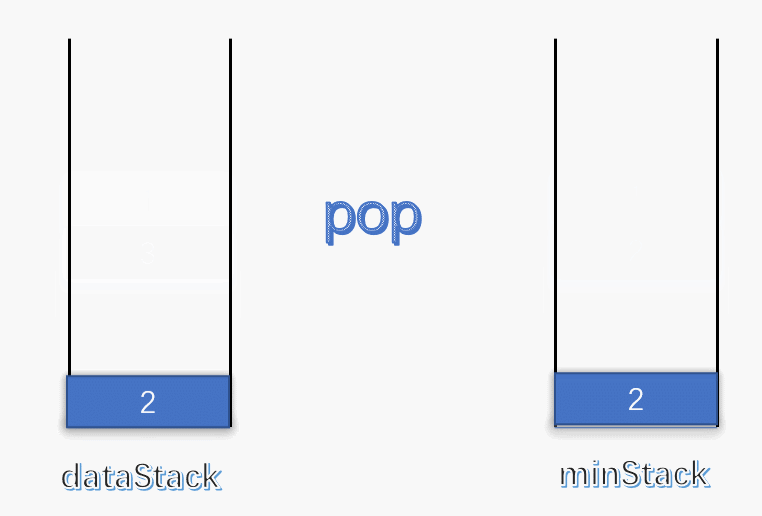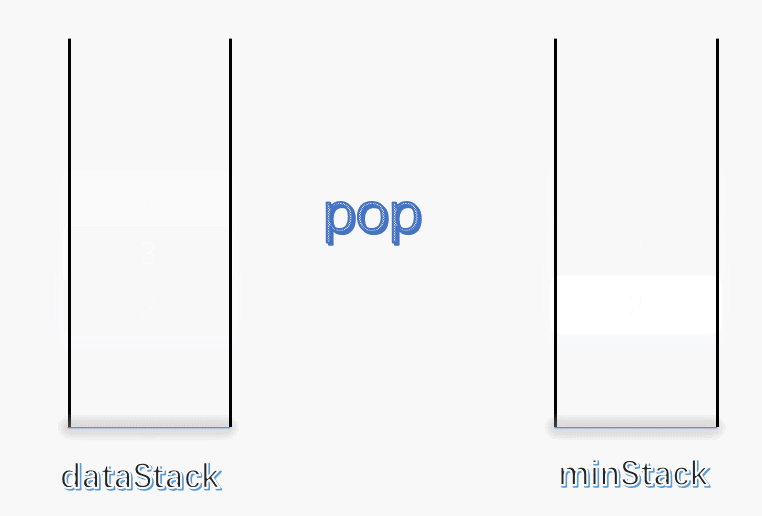
class MinStack { stack<int > minStack; stack<int > dataStack; public : MinStack () { while (!dataStack.empty ()) dataStack.pop (); while (!minStack.empty ()) minStack.pop (); minStack.push (INT_MAX); } void push (int x) dataStack.push (x); minStack.push (std::min (x, minStack.top ())); } void pop () dataStack.pop (); minStack.pop (); } int top () return dataStack.top (); } int min () return minStack.top (); } };
相交链表[160] 给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:
题目数据 保证 整个链式结构中不存在环。
注意 ,函数返回结果后,链表必须 保持其原始结构 。
自定义评测 :
评测系统 的输入如下(你设计的程序 不适用 此输入):
intersectVal - 相交的起始节点的值。如果不存在相交节点,这一值为 `0````listA` - 第一个链表 listB - 第二个链表skipA - 在 listA 中(从头节点开始)跳到交叉节点的节点数skipB - 在 listB 中(从头节点开始)跳到交叉节点的节点数评测系统将根据这些输入创建链式数据结构,并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点,那么你的解决方案将被 视作正确答案 。
示例 1
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3 输出:Intersected at '8' 解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。 从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。 在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例 2
输入:intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1 输出:Intersected at '2' 解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。 从各自的表头开始算起,链表 A 为 [1,9,1,2,4],链表 B 为 [3,2,4]。 在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例3
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2 输出:null 解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。 由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。 这两个链表不相交,因此返回 null 。
提示 listA 中节点数目为 mlistB 中节点数目为 n1 <= m, n <= 3 * 10^41 <= Node.val <= 10^50 <= skipA <= m0 <= skipB <= n如果 listA 和 listB 没有交点,intersectVal 为 0 如果 listA 和 listB 有交点,intersectVal == listA[skipA] == listB[skipB] 进阶: 你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案?
模板 class Solution {public : ListNode *getIntersectionNode (ListNode *headA, ListNode *headB) { } };
题解 使用双指针 ,细想就会发现很简单很巧妙。
A 和 B 两个链表长度可能不同,但是 A + B 和 B + A 的长度是相同的,所以遍历 A + B 和遍历 B + A 一定是同时结束:
class Solution {public : ListNode *getIntersectionNode (ListNode *headA, ListNode *headB) { ListNode* pa = headA; ListNode* pb = headB; while (pa != pb) { pa = pa? pa->next: headB; pb = pb? pb->next: headA; } return pa; } };
两数之和 II - 输入有序数组[167] 给定一个已按照 非递减顺序排列 的整数数组 numbers ,请你从数组中找出两个数满足相加之和等于目标数 target 。
函数应该以长度为 2 的整数数组的形式返回这两个数的下标值。numbers 的下标 从 1 开始计数 ,所以答案数组应当满足 1 <= answer[0] < answer[1] <= numbers.length。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
示例 1 输入:numbers = [2,7,11,15], target = 9 输出:[1,2] 解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。
示例 2 输入:numbers = [2,3,4], target = 6 输出:[1,3]
示例 3 输入:numbers = [-1,0], target = -1 输出:[1,2]
提示 2 <= numbers.length <= 3 * $10^4$ -1000 <= numbers[i] <= 1000 numbers 按 非递减顺序 排列 -1000 <= target <= 1000 仅存在一个有效答案 模板 class Solution {public : vector<int > twoSum (vector<int >& numbers, int target) { } };
题解 双指针:
class Solution {public : vector<int > twoSum (vector<int >& numbers, int target) { int i = 0 ; int j = numbers.size () - 1 ; vector<int > res; while (i < j && numbers[i] + numbers[j] != target) { if (numbers[i] + numbers[j] < target) i++; else j--; } res.push_back (i + 1 ); res.push_back (j + 1 ); return res; } };
二叉树的右视图[199] 给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1 输入: [1,2,3,null,5,null,4] 输出: [1,3,4]
示例 2 示例 3 提示 二叉树的节点个数的范围是 [0,100] -100 <= Node.val <= 100模板 class Solution {public : vector<int > rightSideView (TreeNode* root) { } };
题解 只需将保存每一层最左端的节点值,改为保存每一层最右端的节点值并保存即可。
代码如下,注意空根节点的判断。
class Solution {public : vector<int > rightSideView (TreeNode* root) { vector<int > res; if (!root) return res; queue<TreeNode*> q; q.push (root); while (!q.empty ()) { int size = q.size (); for (int i = 0 ; i < size; i++) { TreeNode* node = q.front (); q.pop (); if (i == size - 1 ) res.push_back (node->val); if (node->left) q.push (node->left); if (node->right) q.push (node->right); } } return res; } };
反转链表[206] 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1
输入:head = [1,2,3,4,5] 输出:[5,4,3,2,1]
示例 2
示例3 提示 链表中节点的数目范围是 [0, 5000] -5000 <= Node.val <= 5000 模板 class Solution {public : ListNode* reverseList (ListNode* head) { } };
题解 递归 考虑使用递归法遍历链表,当越过尾节点后终止递归,在回溯时修改各节点的 next 引用指向。
class Solution {public : ListNode* reverseList (ListNode* head) { if (!head || !head->next) return head; else { ListNode* res = reverseList (head->next); ListNode* tmp = head->next->next; head->next->next = head; head->next = nullptr ; return res; } } };
非递归 非递归方法我选择直接背诵了,可以看到几个等式成一个环状收尾相连:
succ--cur->next--pre--cur--succ
完整代码如下:
class Solution {public : ListNode* reverseList (ListNode* head) { ListNode* cur = head; ListNode* pre = nullptr ; ListNode* succ = nullptr ; while (cur) { succ = cur->next; cur->next = pre; pre = cur; cur = succ; } return pre; } };
长度最小的子数组[209] 给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr],并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1 输入:target = 7, nums = [2,3,1,2,4,3] 输出:2 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2 输入:target = 4, nums = [1,4,4] 输出:1
示例 3 输入:target = 11, nums = [1,1,1,1,1,1,1,1] 输出:0
提示 1 <= target <= 10^91 <= nums.length <= 10^51 <= nums[i] <= 10^5进阶 :如果你已经实现 $O(n)$ 时间复杂度的解法, 请尝试设计一个 $O(n log(n))$ 时间复杂度的解法。
模板 class Solution {public : int minSubArrayLen (int target, vector<int >& nums) } };
题解 同向双指针,注意边界条件:
class Solution {public : int minSubArrayLen (int target, vector<int >& nums) int left = 0 , right; int sum = 0 ; int minlen = INT_MAX; for (right = 0 ; right < nums.size (); right++) { sum += nums[right]; while (left <= right && sum >= target) { minlen = min (minlen, right - left + 1 ); sum -= nums[left++]; } } return minlen == INT_MAX? 0 : minlen; } };
回文链表[234] 给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。
示例1
输入:head = [1,2,2,1] 输出:true
示例2
提示 链表中节点数目在范围 [1, 10^5] 内 0 <= Node.val <= 9进阶 :你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?
模板 class Solution {public : bool isPalindrome (ListNode* head) } };
题解 先用快慢指针找到链表的中点,接着反转右半部分的链表。然后同时遍历前后两段链表,若前后两段链表节点对应的值不等,说明不是回文链表,否则说明是回文链表。
class Solution {public : bool isPalindrome (ListNode* head) if (head->next == nullptr ) return true ; ListNode* dummy = new ListNode (); dummy->next = head; ListNode* slow = dummy; ListNode* fast = dummy; while (fast && fast->next) { slow = slow->next; fast = fast->next->next; } ListNode* cur = dummy->next; ListNode* mid = slow->next; slow->next = nullptr ; mid = reverseList (mid); while (mid) { if (cur->val != mid->val) return false ; cur = cur->next; mid = mid->next; } return true ; } ListNode* reverseList (ListNode* head) { ListNode* cur = head; ListNode* pre = nullptr ; ListNode* succ = nullptr ; while (cur) { succ = cur->next; cur->next = pre; pre = cur; cur = succ; } return pre; } };
删除链表中的节点[237] 请编写一个函数,使其可以删除某个链表中给定的(非末尾)节点。传入函数的唯一参数为 要被删除的节点 。
现有一个链表 – head = [4,5,1,9],它可以表示为:
示例 1 输入:head = [4,5,1,9], node = 5 输出:[4,1,9] 解释:给定你链表中值为 5 的第二个节点,那么在调用了你的函数之后,该链表应变为 4 -> 1 -> 9.
示例 2 输入:head = [4,5,1,9], node = 1 输出:[4,5,9] 解释:给定你链表中值为 1 的第三个节点,那么在调用了你的函数之后,该链表应变为 4 -> 5 -> 9.
提示 链表至少包含两个节点 链表中所有节点的值都是唯一的 给定的节点为非末尾节点并且一定是链表中的一个有效节点 不要从你的函数中返回任何结果 模板 class Solution {public : void deleteNode (ListNode* node) } };
题解 方法:与下一个节点交换
从链表里删除一个节点 node 的最常见方法是修改之前节点的 next 指针,使其指向之后的节点。
因为,我们无法访问我们想要删除的节点 之前 的节点,我们始终不能修改该节点的 next 指针。相反,我们必须将想要删除的节点的值替换为它后面节点中的值,然后删除它之后的节点。
class Solution {public : void deleteNode (ListNode* node) node->val = node->next->val; node->next = node->next->next; } };
要说明的是这道题在我看来并不是一道好题,忽略了诸如内存泄漏,删除指针,释放内存这些 C++ 中非常常见的实际问题。
有效的字母异位词[242] 给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。
示例 1 输入: s = "anagram", t = "nagaram" 输出: true
示例 2 输入: s = "rat", t = "car" 输出: false
提示 1 <= s.length, t.length <= 5 * 10^4s 和 t 仅包含小写字母进阶 : 如果输入字符串包含 unicode 字符怎么办?你能否调整你的解法来应对这种情况?
模板 class Solution {public : bool isAnagram (string s, string t) } };
题解 数组或哈希表累加 s 中每个字符出现的次数,再减去 t 中对应的每个字符出现的次数。遍历结束后,若字符中出现次数不为 0 的情况,返回 false,否则返回 true。
class Solution {public : bool isAnagram (string s, string t) if (s.size () != t.size ()) return false ; vector<int > hash (26 , 0 ) , zero (26 , 0 ) ; for (int i = 0 ; i < t.size (); i++) { hash[t[i] - 'a' ]++; hash[s[i] - 'a' ]--; } if (hash == zero) return true ; return false ; } };
移动零[283] 给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
示例 输入: [0,1,0,3,12] 输出: [1,3,12,0,0]
说明 必须在原数组上操作,不能拷贝额外的数组。 尽量减少操作次数。 模板 class Solution {public : void moveZeroes (vector<int >& nums) } };
题解 使用双指针,左指针指向当前已经处理好的序列的尾部,右指针指向待处理序列的头部。
右指针不断向右移动,每次右指针指向非零数,则将左右指针对应的数交换,同时左指针右移。
注意到以下性质:
左指针左边均为非零数; 右指针左边直到左指针处均为零。 因此每次交换,都是将左指针的零与右指针的非零数交换,且非零数的相对顺序并未改变。
class Solution {public : void moveZeroes (vector<int >& nums) int i = 0 , j = 0 ; while (j < nums.size ()) { if (nums[j]) { swap (nums[i], nums[j]); i++; } j++; } } };
二维区域和检索 - 矩阵不可变[304] 给定一个二维矩阵 matrix,以下类型的多个请求:
计算其子矩形范围内元素的总和,该子矩阵的 左上角 为 (row1, col1) ,右下角 为 (row2, col2)。
实现 NumMatrix 类:
NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。示例 1
输入: ["NumMatrix","sumRegion","sumRegion","sumRegion"] [[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]] 输出: [null, 8, 11, 12] 解释: NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]); numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和) numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和) numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)
提示 m == matrix.lengthn == matrix[i].length1 <= m, n <= 200-10^5 <= matrix[i][j] <= 10^50 <= row1 <= row2 < m0 <= col1 <= col2 < n最多调用 10^4 次 sumRegion 方法 模板 class NumMatrix {public : NumMatrix (vector<vector<int >>& matrix) { } int sumRegion (int row1, int col1, int row2, int col2) } };
题解 动态规划-二维前缀和。
class NumMatrix {private : vector<vector<int >> presum; public : NumMatrix (vector<vector<int >>& matrix) { if (!matrix.size () || !matrix[0 ].size ()) return ; presum.resize (matrix.size () + 1 , vector <int >(matrix[0 ].size () + 1 , 0 )); for (int i = 0 ; i < matrix.size (); i++) { int rowsum = 0 ; for (int j = 0 ; j < matrix[0 ].size (); j++) { rowsum += matrix[i][j]; presum[i + 1 ][j + 1 ] = presum[i][j + 1 ] + rowsum; } } } int sumRegion (int row1, int col1, int row2, int col2) return presum[row2 + 1 ][col2 + 1 ] - presum[row1][col2 + 1 ] - presum[row2 + 1 ][col1] + presum[row1][col1]; } };
最大单词长度乘积[318] 给定一个字符串数组 words,找到 length(word[i]) * length(word[j]) 的最大值,并且这两个单词不含有公共字母。你可以认为每个单词只包含小写字母。如果不存在这样的两个单词,返回 0。
示例 1 输入: ["abcw","baz","foo","bar","xtfn","abcdef"] 输出: 16 解释: 这两个单词为 "abcw", "xtfn"。
示例 2 输入: ["a","ab","abc","d","cd","bcd","abcd"] 输出: 4 解释: 这两个单词为 "ab", "cd"。
示例 3 输入: ["a","aa","aaa","aaaa"] 输出: 0 解释: 不存在这样的两个单词。
提示 2 <= words.length <= 1000 1 <= words[i].length <= 1000 words[i] 仅包含小写字母模板 class Solution {public : int maxProduct (vector<string>& words) } };
题解 因为只有 26 个小写字符,所以可以用一个哈希表存储字符的出现情况,然后枚举最大乘积:
class Solution {public : int maxProduct (vector<string>& words) vector<vector<bool >> hash (words.size (), vector <bool >(26 , false )); for (int i = 0 ; i < words.size (); i++) for (char c: words[i]) hash[i][c - 'a' ] = true ; int res = 0 ; for (int i = 0 ; i < words.size (); i++) { for (int j = i + 1 ; j < words.size (); j++) { int k = 0 ; for (; k < 26 ; k++) { if (hash[i][k] && hash[j][k]) break ; } if (k == 26 ) { int prod = words[i].size () * words[j].size (); res = max (res, prod); } } } return res; } };
比特位计数[338] 给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
示例 1 输入:n = 2 输出:[0,1,1] 解释: 0 --> 0 1 --> 1 2 --> 10
示例 2 输入:n = 5 输出:[0,1,1,2,1,2] 解释: 0 --> 0 1 --> 1 2 --> 10 3 --> 11 4 --> 100 5 --> 101
提示 进阶 很容易就能实现时间复杂度为 $O(n log n)$ 的解决方案,你可以在线性时间复杂度 $O(n)$ 内用一趟扫描解决此问题吗? 你能不使用任何内置函数解决此问题吗?(如,C++ 中的 __builtin_popcount ) 模板 class Solution {public : vector<int > countBits (int n) { } };
题解 最直观的做法是对从 $0$ 到 $n$ 的每个整数直接计算「一比特数」。每个 $\texttt{int}$ 型的数都可以用 32 位二进制数表示,只要遍历其二进制表示的每一位即可得到 1 的数目。
利用 $\text{Brian Kernighan}$ 算法,可以在一定程度上进一步提升计算速度。$\text{Brian Kernighan}$ 算法的原理是:对于任意整数 $x$,令 $x=x&(x-1)$,该运算将 $x$ 的二进制表示的最后一个 1 变成 0。因此,对 $x$ 重复该操作,直到 $x$ 变成 $0$,则操作次数即为 $x$ 的「一比特数」。
对于给定的 $n$,计算从 $0$ 到 $n$ 的每个整数的「一比特数」的时间都不会超过 $O(\log n)$,因此总时间复杂度为 $O(n \log n)$。
class Solution {public : vector<int > countBits (int n) { vector<int > res (n + 1 ) ; for (int i = 1 ; i <= n; i++) { res[i] = res[i & (i - 1 )] + 1 ; } return res; } };
反转字符串[344] 编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。
示例 1 输入:["h","e","l","l","o"] 输出:["o","l","l","e","h"]
示例 2 输入:["H","a","n","n","a","h"] 输出:["h","a","n","n","a","H"]
默认模板 class Solution {public : void reverseString (vector<char >& s) } };
题解 这是一道很经典的字符串反转问题,如果可以使用上文的双指针套路,那么应该采取同向还是反向呢?根据观察调换字符串的规律,我们发现只要从外往里,不断调换头部和尾部的元素就能颠倒一个字符串,那很明显和我们提到的反向双指针相关。
class Solution {public : void reverseString (vector<char >& s) int i = 0 , j = s.size () - 1 ; while (i < j) { swap (s[i], s[j]); i++; j--; } } };
数据流中的移动平均值[346] 给定一个整数数据流和一个窗口大小,根据该滑动窗口的大小,计算其所有整数的移动平均值。
实现 MovingAverage 类:
MovingAverage(int size) 用窗口大小 size 初始化对象。double next(int val) 计算并返回数据流中最后 size 个值的移动平均值。示例 输入: ["MovingAverage", "next", "next", "next", "next"] [[3], [1], [10], [3], [5]] 输出: [null, 1.0, 5.5, 4.66667, 6.0] 解释: MovingAverage movingAverage = new MovingAverage(3); movingAverage.next(1); // 返回 1.0 = 1 / 1 movingAverage.next(10); // 返回 5.5 = (1 + 10) / 2 movingAverage.next(3); // 返回 4.66667 = (1 + 10 + 3) / 3 movingAverage.next(5); // 返回 6.0 = (10 + 3 + 5) / 3
提示 1 <= size <= 1000-10^5 <= val <= 10^5最多调用 next 方法 10^4 次 模板 class MovingAverage {public : MovingAverage (int size) { } double next (int val) } };
题解
class MovingAverage { int sum = 0 ; int capacity = 0 ; queue<int > q; public : MovingAverage (int size) { capacity = size; } double next (int val) q.push (val); sum += val; if (q.size () > capacity) { sum -= q.front (); q.pop (); } return double (sum)/ q.size (); } };
O(1) 时间插入、删除和获取随机元素[380] 实现 RandomizedSet 类:
RandomizedSet() 初始化 RandomizedSet 对象bool insert(int val) 当元素 val 不存在时,向集合中插入该项,并返回 true;否则,返回 falsebool remove(int val) 当元素 val 存在时,从集合中移除该项,并返回 true;否则,返回 falseint getRandom() 随机返回现有集合中的一项(测试用例保证调用此方法时集合中至少存在一个元素)。每个元素应该有 相同的概率 被返回你必须实现类的所有函数,并满足每个函数的 平均 时间复杂度为 O(1)
示例 输入 ["RandomizedSet", "insert", "remove", "insert", "getRandom", "remove", "insert", "getRandom"] [[], [1], [2], [2], [], [1], [2], []] 输出 [null, true, false, true, 2, true, false, 2] 解释 RandomizedSet randomizedSet = new RandomizedSet(); randomizedSet.insert(1); // 向集合中插入 1 。返回 true 表示 1 被成功地插入。 randomizedSet.remove(2); // 返回 false ,表示集合中不存在 2 。 randomizedSet.insert(2); // 向集合中插入 2 。返回 true 。集合现在包含 [1,2] 。 randomizedSet.getRandom(); // getRandom 应随机返回 1 或 2 。 randomizedSet.remove(1); // 从集合中移除 1 ,返回 true 。集合现在包含 [2] 。 randomizedSet.insert(2); // 2 已在集合中,所以返回 false 。 randomizedSet.getRandom(); // 由于 2 是集合中唯一的数字,getRandom 总是返回 2 。
提示 -2^31 <= val <= 2^31 - 1 最多调用 insert、remove 和 getRandom 函数 2 * 10^5 次 在调用 getRandom 方法时,数据结构中 至少存在一个 元素。 模板 class RandomizedSet {public : RandomizedSet () { } bool insert (int val) } bool remove (int val) } int getRandom () } };
题解 由于题目要求删除和插入的时间复杂度为 O(1),能够满足要求的只有哈希表,显然此处需要使用哈希表。
但是使用哈希表无法等概率返回其中的每个数值。若这些数值是保存在数组内,则可以轻松解决。但若只使用数组,那么删除和插入一个值时,都需遍历一遍数组找到数值对应的下标,则会使时间复杂度为 O(n)。
故可将哈希表和数组结合,数组内存数值实现 getRandom,哈希内存数值和下标的映射实现 insert 和 remove 的索引查找的时间复杂度为 O(1),之后在数组内操作数值的插入和删除。具体来看操作就是:
插入 每次添加新数值时,先使用哈希表判断该数值是否存在,存在则直接返回 false。不存在则进行插入操作,只要将该数值添加到数组尾部即可,并将该数值和其下标的映射存入哈希表。
删除 删除同样需使用哈希表判断是否存在,若不存在则返回 false。存在则进行删除操作,在哈希表中删除时间复杂度为 O(1),但是在数值中删除比较麻烦。若只是直接删除,则为了保证数组内存连续性需将删除数值后面的数值均前移一位,时间复杂度为 O(n)。比较好的处理方式是,用数组的最后一个数值去填充需要删除的数值的内存,其他数值在数组中的位置保持不变,并将这个拿来填充的数值的下标更新即可,最后只要删除数组最后一个数值,同样可以保证时间复杂度为 O(1)。
随机返回 只要随机生成数组下标范围内一个随机下标值,返回该数组下标内的数值即可。
class RandomizedSet { unordered_map<int , int > mp; vector<int > nums; public : RandomizedSet () { } bool insert (int val) if (mp.count (val)) return false ; mp[val] = nums.size (); nums.push_back (val); return true ; } bool remove (int val) if (!mp.count (val)) return false ; int removeIndex = mp[val]; nums[removeIndex] = nums.back (); mp[nums.back ()] = removeIndex; mp.erase (val); nums.pop_back (); return true ; } int getRandom () return nums[rand () % nums.size ()]; } };
扁平化多级双向链表[430] 多级双向链表中,除了指向下一个节点和前一个节点指针之外,它还有一个子链表指针,可能指向单独的双向链表。这些子列表也可能会有一个或多个自己的子项,依此类推,生成多级数据结构,如下面的示例所示。
给你位于列表第一级的头节点,请你扁平化列表,使所有结点出现在单级双链表中。
示例 1 输入:head = [1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12] 输出:[1,2,3,7,8,11,12,9,10,4,5,6]
示例 2 输入:head = [1,2,null,3] 输出:[1,3,2] 解释: 输入的多级列表如下图所示: 1---2---NULL | 3---NULL
示例 3 如何表示测试用例中的多级链表?
以 示例 1 为例:
1---2---3---4---5---6--NULL | 7---8---9---10--NULL | 11--12--NULL
序列化其中的每一级之后:
[1,2,3,4,5,6,null] [7,8,9,10,null] [11,12,null]
为了将每一级都序列化到一起,我们需要每一级中添加值为 null 的元素,以表示没有节点连接到上一级的上级节点。
[1,2,3,4,5,6,null] [null,null,7,8,9,10,null] [null,11,12,null]
合并所有序列化结果,并去除末尾的 null 。
[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12]
提示 节点数目不超过 1000 1 <= Node.val <= 10^5模板 class Solution {public : Node* flatten (Node* head) { } };
题解 仔细观察一下这个结构,不难发现其实就是前序遍历二叉树:
class Solution {public : Node* flatten (Node* head) { flattenGetTail (head); return head; } Node* flattenGetTail (Node* head) { Node* cur = head; Node* tail = nullptr ; while (cur) { Node* next = cur->next; if (cur->child) { Node* child = cur->child; Node* childTail = flattenGetTail (cur->child); cur->child = nullptr ; cur->next = child; child->prev = cur; childTail->next = next; if (next) next->prev = childTail; tail = childTail; } else { tail = cur; } cur = next; } return tail; } };
找到字符串中所有字母异位词[438] 给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
示例 1 输入: s = "cbaebabacd", p = "abc" 输出: [0,6] 解释: 起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。 起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。
示例 2 输入: s = "abab", p = "ab" 输出: [0,1,2] 解释: 起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。 起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。 起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。
提示 1 <= s.length, p.length <= 3 * 104s 和 p 仅包含小写字母模板 class Solution {public : vector<int > findAnagrams (string s, string p) { } };
题解 滑动窗口。
class Solution {public : vector<int > findAnagrams (string s, string p) { vector<int > res; vector<int > hash (26 , 0 ) , zero (26 , 0 ) ; if (p.size () > s.size ()) return res; for (int i = 0 ; i < p.size (); i++) { hash[p[i] - 'a' ]++; hash[s[i] - 'a' ]--; } if (hash == zero) res.push_back (0 ); for (int i = p.size (); i < s.size (); i++) { hash[s[i] - 'a' ]--; hash[s[i - p.size ()] - 'a' ]++; if (hash == zero) res.push_back (i - p.size () + 1 ); } return res; } };
两数相加 II[445] 给定两个 非空链表 l1和 l2 来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。
可以假设除了数字 0 之外,这两个数字都不会以零开头。
示例1
输入:l1 = [7,2,4,3], l2 = [5,6,4] 输出:[7,8,0,7]
示例2 输入:l1 = [2,4,3], l2 = [5,6,4] 输出:[8,0,7]
示例3 输入:l1 = [0], l2 = [0] 输出:[0]
提示 链表的长度范围为[1, 100] 0 <= node.val <= 9输入数据保证链表代表的数字无前导 0 进阶: 如果输入链表不能修改该如何处理?换句话说,不能对列表中的节点进行翻转。
模板 class Solution {public : ListNode* addTwoNumbers (ListNode* l1, ListNode* l2) { } };
题解 对链表进行翻转 设置一个空节点 dummy,也就是末尾节点,和一个进位数 carry 遍历链表 l1、l2,条件是链表1,2不为空和进位数大于 0 求出当前位数,生成节点 对当前节点的 next 指向上一个节点(逆序)和求进位到下一个的数 三目运算符对链表进行下一个指向判断 class Solution {public : ListNode* addTwoNumbers (ListNode* l1, ListNode* l2) { int carry = 0 ; l1 = reverse (l1); l2 = reverse (l2); ListNode* dummy = new ListNode (0 ); ListNode* l = dummy; while (l1 || l2) { int sum = (l1? l1->val: 0 ) + (l2? l2->val: 0 ) + carry; carry = sum >= 10 ? 1 : 0 ; sum = sum >= 10 ? sum - 10 : sum; l->next = new ListNode (sum); l = l->next; l1 = l1? l1->next: nullptr ; l2 = l2? l2->next: nullptr ; } if (carry) l->next = new ListNode (carry); return reverse (dummy->next); } ListNode* reverse (ListNode* head) { ListNode* cur = head; ListNode* pre = nullptr ; ListNode* succ = nullptr ; while (cur) { succ = cur->next; cur->next = pre; pre = cur; cur = succ; } return pre; } };
找树左下角的值[513] 给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
示例 1
示例 2
输入: [1,2,3,4,null,5,6,null,null,7] 输出: 7
提示: 二叉树的节点个数的范围是 [1,10^4] -2^31 <= Node.val <= 2^31 - 1模板 class Solution {public : int findBottomLeftValue (TreeNode* root) } };
题解 若每次都记录当前层的最左端值,那么等遍历完二叉树,记录的当前层的最左端节点值就是最底层的最左端节点值,如图所示。
class Solution {public : int findBottomLeftValue (TreeNode* root) queue<TreeNode*> q; q.push (root); int bottomLeft = 0 ; while (!q.empty ()) { int size = q.size (); for (int i = 0 ; i < size; i++) { TreeNode* node = q.front (); q.pop (); if (i == 0 ) bottomLeft = node->val; if (node->left) q.push (node->left); if (node->right) q.push (node->right); } } return bottomLeft; } };
在每个树行中找最大值[515] 给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
示例1 输入: root = [1,3,2,5,3,null,9] 输出: [1,3,9] 解释: 1 / \ 3 2 / \ \ 5 3 9
示例2 输入: root = [1,2,3] 输出: [1,3] 解释: 1 / \ 2 3
示例3 示例4 输入: root = [1,null,2] 输出: [1,2] 解释: 1 \ 2
示例5 提示 二叉树的节点个数的范围是 [0,10^4] -2^31 <= Node.val <= 2^31 - 1模板 class Solution {public : vector<int > largestValues (TreeNode* root) { } };
题解
“BFS 层次遍历”实现。
因为要求解二叉树每一层的最大值,所以使用二叉树的层次遍历是最适合不过的。但是因为需要求二叉树的每一层的最大值,所以需要确定哪些节点属于同一层。一种简单的方式就是,在遍历完当前层的最后一个节点之后,队列中所保存的节点数就是下一层的节点数。如图所示,红色节点为当前层的最后一个节点,绿色为处于队列中的下一层的所有节点。因为队列的初始状态是只有一个不为空的根节点,所以第一层就是一个节点,第二次就是遍历完根节点之后的队列中的节点,以此类推。
class Solution {public : vector<int > largestValues (TreeNode* root) { int cur = 0 ; int next = 0 ; int max = INT_MIN; vector<int > res; queue<TreeNode*> q; if (root) { q.push (root); cur = 1 ; } while (!q.empty ()) { TreeNode* node = q.front (); q.pop (); cur--; max = std::max (max, node->val); if (node->left) { q.push (node->left); next++; } if (node->right) { q.push (node->right); next++; } if (cur == 0 ) { res.push_back (max); max = INT_MIN; cur = next; next = 0 ; } } return res; } };
连续数组[525] 给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。
示例 1 输入: nums = [0,1] 输出: 2 说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。
示例 2 输入: nums = [0,1,0] 输出: 2 说明: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。
提示 1 <= nums.length <= 10^5 nums[i] 不是 0 就是 1 模板 class Solution {public : int findMaxLength (vector<int >& nums) } };
题解 前缀和加哈希表,把 0 当作 -1 处理,题目变成求和为 0 的子数组:
class Solution {public : int findMaxLength (vector<int >& nums) int presum = 0 ; int maxlen = 0 ; unordered_map<int , int > mp; mp[0 ] = -1 ; for (int i = 0 ; i < nums.size (); i++) { presum += nums[i] == 0 ? -1 : 1 ; if (mp.find (presum) != mp.end ()) maxlen = max (maxlen, i - mp[presum]); else mp[presum] = i; } return maxlen; } };
最小时间差[539] 给定一个 24 小时制(小时:分钟 **”HH:MM”**)的时间列表,找出列表中任意两个时间的最小时间差并以分钟数表示。
示例 1 输入:timePoints = ["23:59","00:00"] 输出:1
示例 2 输入:timePoints = ["00:00","23:59","00:00"] 输出:0
提示 2 <= timePoints <= 2 * 10^4timePoints[i] 格式为 “HH:MM “模板 class Solution {public : int findMinDifference (vector<string>& timePoints) } };
题解 首先,遍历时间列表,将其转换为“分钟制”列表 mins,比如,对于时间点 13:14,将其转换为 13 * 60 + 14。
接着将“分钟制”列表按升序排列,然后将此列表的最小时间 mins[0] 加上 24 * 60 追加至列表尾部,用于处理最大值、最小值的差值这种特殊情况。
最后遍历“分钟制”列表,找出相邻两个时间的最小值即可。
class Solution {public : int findMinDifference (vector<string> &timePoints) if (timePoints.size () > 24 * 60 ) return 0 ; vector<int > mins; for (auto t : timePoints) mins.push_back (stoi (t.substr (0 , 2 )) * 60 + stoi (t.substr (3 ))); sort (mins.begin (), mins.end ()); mins.push_back (mins[0 ] + 24 * 60 ); int res = 24 * 60 ; for (int i = 1 ; i < mins.size (); ++i) res = min (res, mins[i] - mins[i - 1 ]); return res; } };
和为 K 的子数组[560] 给你一个整数数组 nums 和一个整数 k ,请你统计并返回该数组中和为 k 的连续子数组的个数。
示例 1 输入:nums = [1,1,1], k = 2 输出:2
示例 2 输入:nums = [1,2,3], k = 3 输出:2
提示 1 <= nums.length <= 2 * 10^4 -1000 <= nums[i] <= 1000 -10^7 <= k <= 10^7 模板 class Solution {public : int subarraySum (vector<int >& nums, int k) } };
题解 数组中既有正数又有负数,无法使用双指针。可以利用前缀和思想,快速判断子数组的和。前缀和思想。遍历数组求前缀和,把前缀和以及这个和出现的次数作为键值对存入哈希表中。
举例理解:数组的前 i 个数字之和记为 sum,如果存在一个 j(j < i),数组的前 j 个数字之和为sum - k,那么数组中从第 j + 1个数字开始到第 i 个数字结束的子数组之和为 k。
class Solution {public : int subarraySum (vector<int >& nums, int k) if (nums.size () < 0 ) return 0 ; int presum = 0 ; int count = 0 ; unordered_map<int , int > mp; mp[0 ] = 1 ; for (int right = 0 ; right < nums.size (); right++) { presum += nums[right]; count += mp[presum - k]; mp[presum]++; } return count; } };
字符串中的变位词[567] 给定两个字符串 s1 和 s2,写一个函数来判断 s2 是否包含 s1 的某个变位词。
换句话说,第一个字符串的排列之一是第二个字符串的 子串 。
示例 1 输入: s1 = "ab" s2 = "eidbaooo" 输出: True 解释: s2 包含 s1 的排列之一 ("ba").
示例 2 输入: s1= "ab" s2 = "eidboaoo" 输出: False
提示 1 <= s1.length, s2.length <= 104s1 和 s2 仅包含小写字母注意:本题与主站 567 题相同: https://leetcode-cn.com/problems/permutation-in-string/
模板 class Solution {public : bool checkInclusion (string s1, string s2) } };
题解 记录 s1 的哈希数组 确定左右指针的初始位置,并将当前所夹的子数组的字符出现情况与 s1 的哈希表进行比较 同时右移左右指针,左指针右移导致 ‘c’ 不在所夹的子数组中,所以将比较后的哈希数组中 ‘c’ 对应的值加 1,右指针右移导致 ‘b’ 进入所夹的子数组中,所以将比较后的哈希数组中 ‘b’ 对应的值减 1 重复步骤 3,直至找到答案或者遍历完 s2 均未找到答案
class Solution {public : bool checkInclusion (string s1, string s2) if (s1.size () > s2.size ()) return false ; vector<int > hash (26 , 0 ) , zero (26 , 0 ) ; for (int i = 0 ; i < s1.size (); i++) { hash[s1[i] - 'a' ]++; hash[s2[i] - 'a' ]--; } if (hash == zero) return true ; for (int i = s1.size (); i < s2.size (); i++) { hash[s2[i] - 'a' ]--; hash[s2[i - s1.size ()] - 'a' ]++; if (hash == zero) return true ; } return false ; } };
循环有序列表的插入[708] 给定循环单调非递减列表中的一个点,写一个函数向这个列表中插入一个新元素 insertVal,使这个列表仍然是循环非降序的。
给定的可以是这个列表中任意一个顶点的指针,并不一定是这个列表中最小元素的指针。
如果有多个满足条件的插入位置,你可以选择任意一个位置插入新的值,插入后整个列表仍然保持有序。
如果列表为空(给定的节点是 null),你需要创建一个循环有序列表并返回这个节点。否则。请返回原先给定的节点。
示例 1
输入:head = [3,4,1], insertVal = 2 输出:[3,4,1,2] 解释:在上图中,有一个包含三个元素的循环有序列表,你获得值为 3 的节点的指针,我们需要向表中插入元素 2 。新插入的节点应该在 1 和 3 之间,插入之后,整个列表如上图所示,最后返回节点 3 。
示例 2 输入:head = [], insertVal = 1 输出:[1] 解释:列表为空(给定的节点是 null),创建一个循环有序列表并返回这个节点。
示例 3 输入:head = [1], insertVal = 0 输出:[1,0]
提示 0 <= Number of Nodes <= 5 * 104-10^6 <= Node.val, insertVal <= 10^6模板 class Solution {public : Node* insert (Node* head, int insertVal) { } };
题解 头节点如果为空或仅为一个,直接返回 head或连成环 如果 insertVal 在链表的最小值和最大值之间,找到合适的位置插入 如果 insertVal 小于链表的最小值或大于链表的最大值,则在头节点和尾节点之间插入 class Solution {public : Node* insert (Node* head, int insertVal) { Node* insert = new Node (insertVal); if (head == nullptr ) { head = insert; head->next = head; } else if (head->next == nullptr ) { head->next = insert; insert->next = head; } else { insertCore (head, insert); } return head; } void insertCore (Node* head, Node* insert) Node* cur = head; Node* maxNode = head; Node* next = head->next; while (!(cur->val <= insert->val && insert->val <= next->val) && next != head) { cur = next; next = next->next; if (cur->val >= maxNode->val) maxNode = cur; } if (cur->val <= insert->val && insert->val <= next->val) { insert->next = next; cur->next = insert; } else { insert->next = maxNode->next; maxNode->next = insert; } } };
乘积小于K的子数组[713] 给定一个正整数数组 nums和整数 k 。
请找出该数组内乘积小于 k 的连续的子数组的个数。
示例 1 输入: nums = [10,5,2,6], k = 100 输出: 8 解释: 8个乘积小于100的子数组分别为: [10], [5], [2], [6], [10,5], [5,2], [2,6], [5,2,6]。 需要注意的是 [10,5,2] 并不是乘积小于100的子数组。
示例 2 输入: nums = [1,2,3], k = 0 输出: 0
提示 1 <= nums.length <= 3 * 10^4 1 <= nums[i] <= 1000 0 <= k <= 10^6 模板 class Solution {public : int numSubarrayProductLessThanK (vector<int >& nums, int k) } };
题解 利用滑动窗口,我们能求出每个不同 right 结尾的合法子数组的个数:
class Solution {public : int numSubarrayProductLessThanK (vector<int >& nums, int k) int left = 0 , right; long mul = 1 ; int count = 0 ; for (right = 0 ; right < nums.size (); right++) { mul *= nums[right]; while (left <= right && mul >= k) { mul /= nums[left++]; } count += right >= left? right - left + 1 : 0 ; } return count; } };
寻找数组的中心下标[724] 给你一个整数数组 nums ,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。
示例 1 输入:nums = [1, 7, 3, 6, 5, 6] 输出:3 解释: 中心下标是 3 。 左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 , 右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ,二者相等。
示例 2 输入:nums = [1, 2, 3] 输出:-1 解释: 数组中不存在满足此条件的中心下标。
示例 3 输入:nums = [2, 1, -1] 输出:0 解释: 中心下标是 0 。 左侧数之和 sum = 0 ,(下标 0 左侧不存在元素), 右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。
提示 1 <= nums.length <= 10^4 -1000 <= nums[i] <= 1000 注意:本题与主站 1991 题相同:https://leetcode-cn.com/problems/find-the-middle-index-in-array/
模板 class Solution {public : int pivotIndex (vector<int >& nums) };
题解 用前缀和进行预处理,避免重复计算:
class Solution {public : int pivotIndex (vector<int >& nums) int sum = 0 ; int total = 0 ; for (int num: nums) sum += num; for (int i = 0 ; i < nums.size (); i++) { total += nums[i]; if (total - nums[i] == sum - total) return i; } return -1 ; } };
行星碰撞[735] 给定一个整数数组 asteroids,表示在同一行的行星。
对于数组中的每一个元素,其绝对值表示行星的大小,正负表示行星的移动方向(正表示向右移动,负表示向左移动)。每一颗行星以相同的速度移动。
找出碰撞后剩下的所有行星。碰撞规则:两个行星相互碰撞,较小的行星会爆炸。如果两颗行星大小相同,则两颗行星都会爆炸。两颗移动方向相同的行星,永远不会发生碰撞。
示例 1 输入:asteroids = [5,10,-5] 输出:[5,10] 解释:10 和 -5 碰撞后只剩下 10 。 5 和 10 永远不会发生碰撞。
示例 2 输入:asteroids = [8,-8] 输出:[] 解释:8 和 -8 碰撞后,两者都发生爆炸。
示例 3 输入:asteroids = [10,2,-5] 输出:[10] 解释:2 和 -5 发生碰撞后剩下 -5 。10 和 -5 发生碰撞后剩下 10 。
示例 4 输入:asteroids = [-2,-1,1,2] 输出:[-2,-1,1,2] 解释:-2 和 -1 向左移动,而 1 和 2 向右移动。 由于移动方向相同的行星不会发生碰撞,所以最终没有行星发生碰撞。
提示 2 <= asteroids.length <= 10^4-1000 <= asteroids[i] <= 1000asteroids[i] != 0模板 class Solution {public : vector<int > asteroidCollision (vector<int >& asteroids) { } };
题解 可以类比成左右括号匹配:
向右移动的小行星(左括号):不会引发碰撞,直接入栈 向左移动的小行星(右括号):可能会和之前向右移动的小行星发生碰撞,特殊处理 因为答案需要碰撞后剩下的所有小行星,相当于栈里最后剩下的元素,所以可以直接用数组表示栈。
class Solution {public : vector<int > asteroidCollision (vector<int >& asteroids) { vector<int > res; for (auto a: asteroids) { if (a > 0 ) { res.push_back (a); } else { while (!res.empty () && res.back () > 0 && res.back () < -a) res.pop_back (); if (!res.empty () && res.back () == -a) res.pop_back (); else if (res.empty () || res.back () < -a) res.push_back (a); } } return res; } };
每日温度[739] 请根据每日 气温 列表 temperatures ,请计算在每一天需要等几天才会有更高的温度。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例1 输入: temperatures = [73,74,75,71,69,72,76,73] 输出: [1,1,4,2,1,1,0,0]
示例2 输入: temperatures = [30,40,50,60] 输出: [1,1,1,0]
示例3 输入: temperatures = [30,60,90] 输出: [1,1,0]
提示 1 <= temperatures.length <= $10^5$ 30 <= temperatures[i] <= 100 模板 class Solution {public : vector<int > dailyTemperatures (vector<int >& temperatures) { } };
题解
如果当前元素比栈顶大,则让小项逐个出栈,直到当前元素比栈顶小,停止出栈 此时的栈顶元素就是当前项右边的第一个比自己大的元素索引,计算距离 当前项入栈 class Solution {public : vector<int > dailyTemperatures (vector<int >& temperatures) { int n = temperatures.size (); stack<int > s; vector<int > res (n) ; for (int i = n - 1 ; i >= 0 ; i--) { while (!s.empty () && temperatures[i] >= temperatures[s.top ()]) s.pop (); if (s.empty ()) res[i] = 0 ; else res[i] = s.top () - i; s.push (i); } return res; } };
链表的中间结点[876] 给定一个头结点为 head 的非空单链表,返回链表的中间结点。
如果有两个中间结点,则返回第二个中间结点。
示例 1 输入:[1,2,3,4,5] 输出:此列表中的结点 3 (序列化形式:[3,4,5]) 返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。 注意,我们返回了一个 ListNode 类型的对象 ans,这样: ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL.
示例 2 输入:[1,2,3,4,5,6] 输出:此列表中的结点 4 (序列化形式:[4,5,6]) 由于该列表有两个中间结点,值分别为 3 和 4,我们返回第二个结点。
提示 模板 class Solution {public : ListNode* middleNode (ListNode* head) { } };
题解 用两个指针 slow 与 fast 一起遍历链表。slow 一次走一步,fast 一次走两步。那么当 fast 到达链表的末尾时,slow 必然位于中间。
class Solution {public : ListNode* middleNode (ListNode* head) { ListNode* slow = head; ListNode* fast = head; while (fast && fast->next) { slow = slow->next; fast = fast->next->next; } return slow; } };
完全二叉树插入器[919] 完全二叉树是每一层(除最后一层外)都是完全填充(即,节点数达到最大)的,并且所有的节点都尽可能地集中在左侧。
设计一个用完全二叉树初始化的数据结构 CBTInserter,它支持以下几种操作:
CBTInserter(TreeNode root) 使用头节点为 root 的给定树初始化该数据结构;CBTInserter.insert(int v) 向树中插入一个新节点,节点类型为 TreeNode,值为 v 。使树保持完全二叉树的状态,并返回插入的新节点的父节点的值;CBTInserter.get_root() 将返回树的头节点。示例 1 输入:inputs = ["CBTInserter","insert","get_root"], inputs = [[[1]],[2],[]] 输出:[null,1,[1,2]]
示例 2 输入:inputs = ["CBTInserter","insert","insert","get_root"], inputs = [[[1,2,3,4,5,6]],[7],[8],[]] 输出:[null,3,4,[1,2,3,4,5,6,7,8]]
提示 最初给定的树是完全二叉树,且包含 1 到 1000 个节点。 每个测试用例最多调用 CBTInserter.insert 操作 10000 次。 给定节点或插入节点的每个值都在 0 到 5000 之间。 模板 class CBTInserter {public : CBTInserter (TreeNode* root) { } int insert (int val) } TreeNode* get_root () { } };
题解 完全二叉树只有最后一层是不满的,通过层序遍历就能找到应该插入的节点位置的父节点,然后将新节点插到该父节点下面即可。
class CBTInserter { TreeNode* rt; queue<TreeNode*> q; public : CBTInserter (TreeNode* root) { rt = root; q.push (rt); while (q.front ()->left && q.front ()->right) { TreeNode* node = q.front (); q.pop (); q.push (node->left); q.push (node->right); } } int insert (int val) TreeNode* parent = q.front (); TreeNode* node = new TreeNode (val); if (parent->left == nullptr ) { parent->left = node; } else { parent->right = node; q.pop (); q.push (parent->left); q.push (parent->right); } return parent->val; } TreeNode* get_root () { return rt; } };
最近的请求次数[933] 写一个 RecentCounter 类来计算特定时间范围内最近的请求。
请你实现 RecentCounter 类:
RecentCounter() 初始化计数器,请求数为 0int ping(int t) 在时间 t 添加一个新请求,其中 t 表示以毫秒为单位的某个时间,并返回过去 3000 毫秒内发生的所有请求数(包括新请求)。确切地说,返回在 [t-3000, t] 内发生的请求数。保证 每次对 ping 的调用都使用比之前更大的 t 值。
示例 输入: ["RecentCounter", "ping", "ping", "ping", "ping"] [[], [1], [100], [3001], [3002]] 输出: [null, 1, 2, 3, 3] 解释: RecentCounter recentCounter = new RecentCounter(); recentCounter.ping(1); // requests = [1],范围是 [-2999,1],返回 1 recentCounter.ping(100); // requests = [1, 100],范围是 [-2900,100],返回 2 recentCounter.ping(3001); // requests = [1, 100, 3001],范围是 [1,3001],返回 3 recentCounter.ping(3002); // requests = [1, 100, 3001, 3002],范围是 [2,3002],返回 3
提示 1 <= t <= 10^9保证每次对 ping 调用所使用的 t 值都 严格递增 至多调用 ping 方法 10^4 次 模板 class RecentCounter {public : RecentCounter () { } int ping (int t) } };
题解 在第 1、100、3001、3002 这四个时间点分别进行了 ping 请求, 在 3001 秒的时候, 它前面的 3000 秒指的是区间 [1,3001], 所以一共是有 1、100、3001 三个请求, t = 3002 的前 3000 秒指的是区间 [2,3002], 所以有 100、3001、3002 三次请求。
可以用队列实现。每次将 t 进入队尾,同时从队头开始依次移除小于 t-3000 的元素。然后返回队列的大小 q.size() 即可。
class RecentCounter { queue<long > q; public : RecentCounter () { } int ping (int t) q.push (t); while (q.front () + 3000 < t) { q.pop (); } return q.size (); } };
验证外星语词典[953] 某种外星语也使用英文小写字母,但可能顺序 order 不同。字母表的顺序(order)是一些小写字母的排列。
给定一组用外星语书写的单词 words,以及其字母表的顺序 order,只有当给定的单词在这种外星语中按字典序排列时,返回 true;否则,返回 false。
示例 1 输入:words = ["hello","leetcode"], order = "hlabcdefgijkmnopqrstuvwxyz" 输出:true 解释:在该语言的字母表中,'h' 位于 'l' 之前,所以单词序列是按字典序排列的。
示例 2 输入:words = ["word","world","row"], order = "worldabcefghijkmnpqstuvxyz" 输出:false 解释:在该语言的字母表中,'d' 位于 'l' 之后,那么 words[0] > words[1],因此单词序列不是按字典序排列的。
示例 3 输入:words = ["apple","app"], order = "abcdefghijklmnopqrstuvwxyz" 输出:false 解释:当前三个字符 "app" 匹配时,第二个字符串相对短一些,然后根据词典编纂规则 "apple" > "app",因为 'l' > '∅',其中 '∅' 是空白字符,定义为比任何其他字符都小(更多信息)。
提示 1 <= words.length <= 1001 <= words[i].length <= 20order.length == 26在 words[i] 和 order 中的所有字符都是英文小写字母。 模板 class Solution {public : bool isAlienSorted (vector<string>& words, string order) } };
题解 用数组或哈希表存放字母顺序。依次遍历单词列表,检测相邻两单词是否满足字典序。
class Solution {public : bool isAlienSorted (vector<string>& words, string order) for (int i = 0 ; i < words.size () - 1 ; i++) { if (!isOrdered (words[i], words[i +1 ], order)) return false ; } return true ; } bool isOrdered (string word1, string word2, string order) vector<int > hash (26 , 0 ) ; for (int i = 0 ; i < 26 ; i++) hash[order[i] - 'a' ] = i; int i; for (i = 0 ; i < word1.size () && i < word2.size (); i++) { char ch1 = word1[i]; char ch2 = word2[i]; if (hash[ch1 - 'a' ] < hash[ch2 - 'a' ]) return true ; else if (hash[ch1 - 'a' ] > hash[ch2 - 'a' ]) return false ; } return i == word1.size (); } };
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()